Retail Banking Customer Default Probability
See this project’s code on GitHub
Abstract
Background: This research focuses on predicting credit card default, specifically examining instances of more than 90 days of past due. Utilizing Exploratory Data Analysis (EDA) and Machine Learning in Python, complemented by graphical representations in Python and Tableau.
Objectives: Identify key factors influencing the probability of default, such as age, debt ratio, monthly income, open credit lines, dependents, and past due occurrences in the past 2 years.
Methods: Employing a Probit model, achieving a 93% accuracy, and an AUC-ROC curve of 0.7, indicating good explanatory power and potential adverse selection of credit card issues up to 7%.
Results: Significant variables include age, debt ratio, monthly income, open credit lines, dependents, and past due occurrences. The Probit model demonstrates a high accuracy of 93%, with the AUC-ROC curve confirming its robust explanatory power.
Conclusion: This research highlights demographic and financial factors crucial for predicting credit card default. The developed Probit model offers a reliable tool, with a 93% accuracy, potentially reducing adverse selection in credit card issuances.
Data
The dataset utilized in this research is the "Give Me Some Credit" dataset, accessible on Kaggle through the following link: https://www.kaggle.com/c/GiveMeSomeCredit/data. This dataset is a comprehensive compilation of credit-related information, offering a rich source for investigating the probability of credit card default. It encompasses various features crucial for predictive modeling, including demographic factors such as age and number of dependents, financial indicators like monthly income and debt ratio, and historical credit behavior, notably past due occurrences within the past 2 years. Leveraging this dataset, the research employs Exploratory Data Analysis (EDA) and machine learning algorithms to uncover patterns and develop a Probit model, contributing to a comprehensive understanding of the factors influencing credit card default probabilities.
Methodology & Results
The initial phase involved meticulous data cleaning, beginning with the removal of missing values to ensure dataset integrity. Subsequently, an Ordinary Least Squares (OLS) regression was implemented, targeting variables with a significance level below 95% (p-value < 0.050). This step aimed to refine the dataset by eliminating statistically insignificant variables.
Following the data cleaning process, the refined dataset, free of dropped values, was employed to develop the Probit model. A test size of 20% (test_size = 0.2) was chosen to partition the data, considering the substantial size of the dataset, allowing for a robust evaluation with a sufficient number of observations.
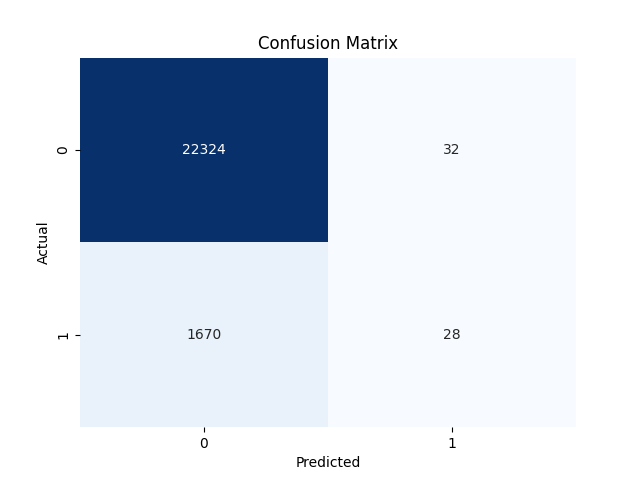
The evaluation of the Probit model yielded a Receiver Operating Characteristic (ROC) curve with an Area Under the Curve (AUC) of 0.7. The associated confusion matrix revealed that the 7% adverse selection is distributed as follows: 0.133% false positives, indicating instances where default was predicted but did not occur, and 6.943% false negatives, signifying cases where default occurred but was not predicted. These results provide insights into the predictive performance of the model and the potential occurrence of adverse selection in credit card issuances.
Decision - Conclusion
In conclusion, this study leverages the "Give Me Some Credit" dataset to explore the probability of credit card default, employing rigorous data cleaning and a Probit model. Through the elimination of missing values and statistically insignificant variables via an Ordinary Least Squares (OLS) regression, a refined dataset was prepared. The Probit model, developed on this cleaned dataset, exhibited an impressive 93% accuracy, underscoring its efficacy in predicting credit card default probabilities. The associated Receiver Operating Characteristic (ROC) curve revealed an Area Under the Curve (AUC) of 0.7, affirming the model's robust explanatory power. Adverse selection, quantified at 7%, was distributed as 0.133% false positives and 6.943% false negatives, emphasizing the model's potential in mitigating adverse selection in credit card issuances. These findings contribute valuable insights into credit risk assessment, offering a reliable tool for informed decision-making in the financial sector.
Those aged between 30 and 50 years old present higher probability of default.
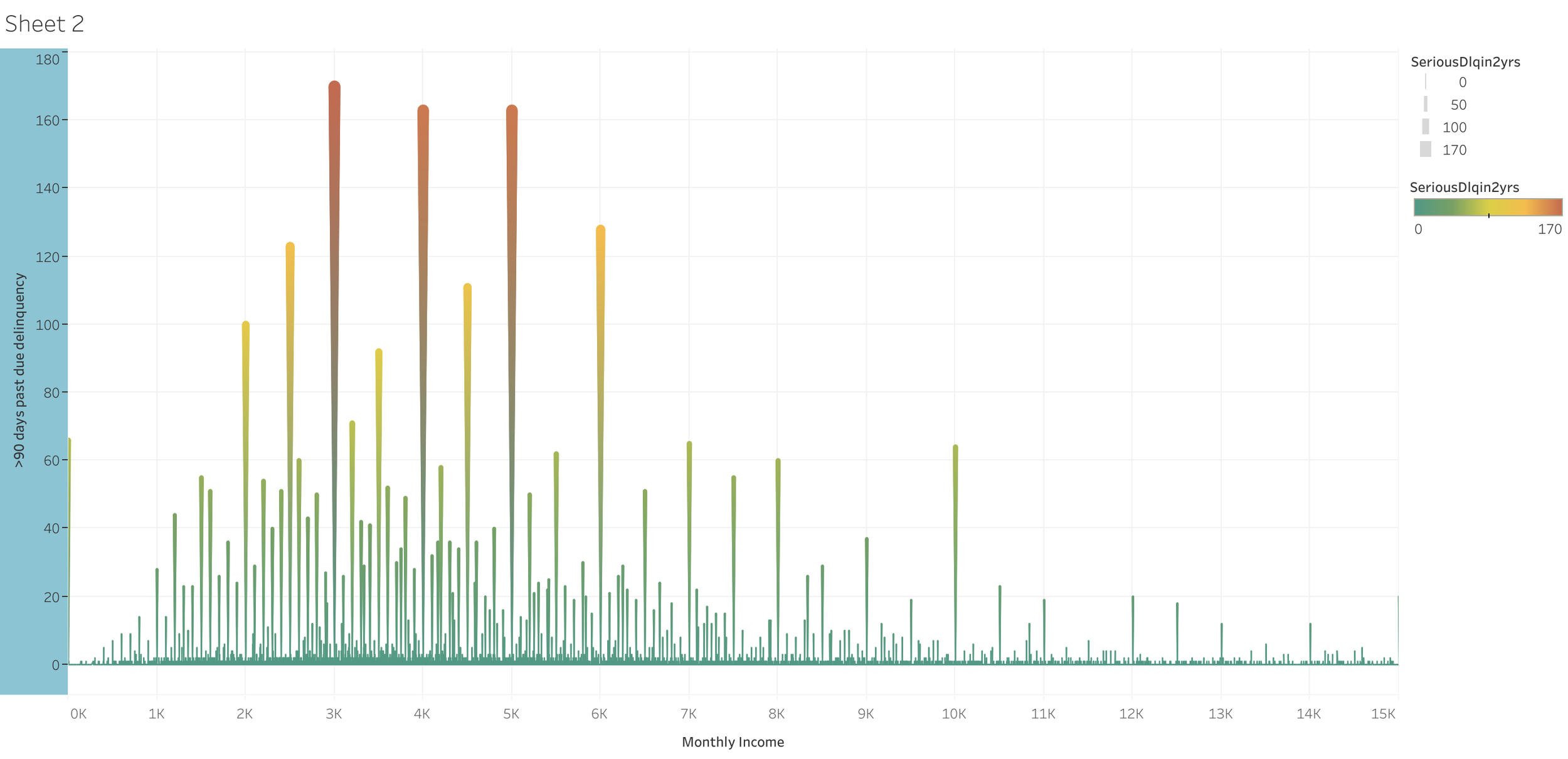
There is higher probability of default for those who have a monthly income of 3.000 - 5.000$
Surprisingly, those without dependents present higher probability of default.